The stats.ComputeStats class

The stats module contains a set of tools to analyze molecular variation data, either represented as Align instances (which have been extensively described in the previous part of the manual) or Site instances (which hold information for a single locus).

Among those tools, stats.ComputeStats is the more complex, and the more rich with functionalities. Most of the statistics can be computed using this class (in general, only the most complex statistics deserve their own function or class, such as part of linkage disequilibrium statistics, which are addressed near the end of this page).

The rationale for defining ComputeStats as a class rather than a standalone function is that it allows more flexibility (the following sections offer an overview of the possibilities) and that it can also be more efficient if a lot of items (alignments or sites) need to be processed in a row.

The basic worflow consists in the following steps, which are developped in the following paragraphs:

1. Create an instance of the class,

2. Set parameters,

3. Enter the list of statistics to be computed,

4. Process one or several alignments or sites.

Options

It is possible to pass parameters values either as arguments of stats.ComputeStats instances, or through their configure() method. The parameters are listed and explained in the documentation of this method. The most important is multi_hits. By default, multi_hits is False, causing all sites that have more than two alleles to be excluded as well. The default parameters might be what you want if you use single-nucleotide polymorphism markers or nucleotide sequence alignments, but certainly not if you use massively multiallelic markers.

To pass parameters, both syntaxes are equivalent:

>>> cs = egglib.stats.ComputeStats()
>>> cs.configure(multi_hits=True)

and

>>> cs = egglib.stats.ComputeStats(multi_hits=True)

Note also that it is also possible to call configure() later at any moment in the workflow. In general, it is recommended to reuse as much as possible objects whenever you perform intensive computations.

List of statistics

Statistics can be specified using the instance method add_stats(). It is possible to call this method several times in a row, it can be called at any time even after analysing data sets, and it is also possible to enter several statistics at once, as shown in the example below:

>>> cs.add_stats('S', 'Pi')
>>> cs.add_stats('D')

Statistics are represented by a code (as a str). A list of tuples matching each code with a short description can be obtained through the instance method list_stats(). A exhaustive notice is availabled in Diversity statistics.

>>> for stat, descr in cs.list_stats():
...     print(stat + ': ' + descr)
ns_site: Number of analyzed samples per site
ns_site_o: Number of analyzed outgroup samples per site
Aing: Number of alleles in ingroup
Aotg: Number of alleles in outgroup
Atot: Number of alleles in whole dataset
As: Number of singleton alleles
Asd: Number of singleton alleles (derived)
R: Allelic richness
thetaIAM: Theta estimator based on He & IAM model
thetaSMM: Theta estimator based on He & SMM model
[...skipped...]

There is a method to add all possible statistics (all_stats()), but note that, obviously, only those that can be computed (depending on the structure of the provided data set) will be computed (others will be set to None).

Note

Even if a statistic can be computed, it does not mean that it should. When analysing data, it can be counter-productive to generate huge tables of statistics among which some (many) may have too much variance to be interpreted anyway.

You can reset the list of statistics using:

>>> cs.clear_stats()

If you are happy with default values of parameters, you are not required to call configure(). However, it is necessary that you enter parameters to be computed, so you have to call add_stats(). Still, it is not an error to skip this step and proceed with analysing data (but in that case you will not get any results).

Processing data

Once needed parameters have been set and needed statistics have been entered, the user can analyze data using the following methods of the ComputeStats instance:

• process_align() to process an Align instance.

• process_site() to process a Site instance.

• process_sites() to process several Site instances.

• process_freq() to process a Freq instance (see below).

These methods are addressed in more details in the following section. By default, they all return a dict containing computed values of statistics corresponding to the analysis of data provided as argument. It is also possible to call them several times and access the results of the analysis of all passed data eventually (see Multiple alignments).

Computing statistics

Single alignment

Computing statistics from a single alignment should be rather straightforward. Assume we have a Fasta file containing a nucleotide alignment. We show below how we would compute a set of standard statistics used in the case of nucleotide sequences from this alignment:

>>> aln1 = egglib.io.from_fasta('align1.fas', labels=True, alphabet = egglib.alphabets.DNA)
>>> struct = egglib.struct_from_labels(aln1, lvl_pop=0, lvl_indiv=1)
>>> cs = egglib.stats.ComputeStats()
>>> cs.set_structure(struct)
>>> cs.add_stats('S', 'thetaW', 'Pi', 'D', 'lseff', 'nseff')
>>> stats = cs.process_align(aln1)
>>> print(aln1.ns, aln1.ls)
101 8942
>>> print(stats)
{'lseff': 3288, 'S': 305, 'thetaW': 59.02529109000289, 'nseff': 99.0, 'Pi': 67.56256441970726, 'D': 0.48870487478046226}

Note that in order to exclude the outgroup sequences from the analysis, we have to import labels and generate an appropriate Structure instance using the method struct_from_labels(). The management of structures is described in the next section. This structure is then imported in the ComputeStats instance using the method set_structure(). As visible in the statistics list, the number of available statistics is much larger than that, but many will be irrelevant for this kind of data (most of them being reported as None because they just can’t be computed). We first printed the ns (number of provided samples) and ls (alignment length) properties of the alignment: there are 101 samples and 8942 sites.

• S is the number of polymorphic sites. Here we have 305 variable sites.

• thetaW (\(\hat{\theta}_W\)) is the so-called Watterson’s estimator of \(\theta = 4N_e\mu\). The value is close to 60 which approaches 0.09 per analysed site (see below).

• Pi (\(\pi\)) is the nucleotide diversity, which is a bit larger.

• D (Tajima’s \(D\)) is positive (+0.49), which is a corollary of Pi being larger than thetaW.

• lseff is the number of sites used for analysis (excluding those with either too many missing data or too many alleles). Here the number is 3288, meaning that 5654 sites have been excluded (mostly because the default is to exclude all sites with any missing data).

• nseff is the average number of used samples among included sites. In our case, since only sites with no missing data at all have been used, the number of samples is 99 because the last two sequences are from the outgroup, but this value can be smaller if the parameter max_missing is larger than 0 (see example in Missing data).

Note

thetaW and Pi are given per gene (that is, they are summed over the total number of analyzed sites). To be expressed per site, they must be divided by the number of sites available for analysis. If all sites have been provided, this value is given by the statistic lseff. But lseff is relevant if only polymorphic or pre-filtered sites have been provided.

Multiple alignments

If you have several separate alignments but you want to obtain global statistics, the instinctive approach would be to concatenate the alignments and use the result in process_align(). There is a much more efficient way (assuming you want to do so with many alignments), described below.

There is a multi option which, if toggled, set ComputeStats to load data in several batches, perform intermediate computations but delay finalisation of statistics computations until all data have been loaded. In that case, you must call results() to actually compute and get statistics:

>>> alnA = aln1.extract(0, 4500)
>>> alnB = aln1.extract(4500, None)
>>> cs.configure(multi=True, struct=struct)
>>> cs.process_align(alnA)
>>> cs.process_align(alnB)
>>> stats = cs.results()
>>> print(stats)
{'thetaW': 59.02529109000289, 'D': 0.48870487478046226, 'nseff': 99.0, 'lseff': 3288, 'Pi': 67.56256441970726, 'S': 305}

The above example just cut the original alignment in two parts, and then processes the two alignments separately. The final dictionary of statistics, as expected, is exactly identical to the one obtained with the full alignment (n.b. even if it was specified before, it is necessary to pass again the structure, because the call to configure() resets all parameters that are not specified).

Phased data

Note that some statistics require that data are phased. That’s the case of all statistics based on haplotype and linkage disequilibrium. If multiple alignments are loaded, it is not ensured that data are phased, even if the number of samples matches. Make sure that your data are REALLY phased if you want to compute these statistics. By default EggLib will calculate them if the data allow it. Note also that all statistics requiring phase entail significantly longer computations when applied to large number of polymorphic sites. These stastistics are also hardly relevant over large genomic regions.

Using individuals sites

Individual sites can be processed as well. They are represented by the class Site. This class is aimed to represent data for any genetic marker such as a single nucleotide polymorphism (SNP), a microsatellite, an encoded insertion/deletion polymorphism, or any other form of genetic variation properly encoded using an appropriate Alphabet instance. The following functions allow to create a Site:

Generator functions	Source of data
site_from_align()	A position in an Align instance.
site_from_list()	A user-provided list of data.
site_from_vcf()	The current data of a VCF parser (see Using VCF files).

Note that each of those functions has a counterpart as a Site method to allow to recycle an existing object.

In the examples of the following paragraphs, we will create sites from the same alignment that we have been using in previous examples. However, in practice the class Site is mostly there for cases when individual sites are available. The small example below shows how to create a Site from a list of allelic values, which is the most simple and intuitive way:

>>> site = egglib.site_from_list(
...     ['C', 'G', 'G', 'C', 'T', 'T', 'G', 'T', 'G', 'G', 'G', 'G'],
...     alphabet=egglib.alphabets.DNA)

Note

When analysing individual sites, it is frequent that more than two alleles are present (except for canonical SNP sites). It can also happen with sequence alignments. If this is the case and you wish to include such sites in the analysis, don’t forget to set the ComputeStats parameter multi_hits to True.

Single site statistics

The code in the next example will clear the list of statistics and specify a list more adapted to single-site analysis, and then will analyse the site at position 66 (which is the 67^th site):

>>> cs.clear_stats()
>>> cs.configure(multi=False, struct=struct)
>>> cs.add_stats('Aing', 'He', 'R')
>>> site = egglib.site_from_align(aln1, 66)
>>> stats = cs.process_site(site)
>>> print(stats)
{'Aing': 3, 'R': 0.02040816326530612, 'He': 0.6233766233766234}

The statistics computed here are:

• Aing: the number of alleles in ingroup (this is a relatively unfrequent case with a SNP with three alleles within a nucleotide alignment).

• R: the allelic richness.

• He: the heterozygosity (which is above 0.5 only because there are three alleles).

Multiple sites statistics

You might be also interested in statistics over several sites. You can load multiple sites in a similar way as for alignments. In the example below we compute, in addition to Aing, R and He, the per-gene statistic D over all sites of the alignment, but we keep on computing statistics on a per-site basis:

>>> cs.add_stats('D', 'Pi')
>>> site = egglib.Site()
>>> for i in range(aln1.ls):
...     site.from_align(aln1,i)
...     stats = cs.process_site(site)
...     print(stats)
{'R': 0.0, 'He': 0.0, 'Pi': None, 'D': None, 'Aing': 1}
{'R': 0.0, 'He': 0.0, 'Pi': None, 'D': None, 'Aing': 1}
[...skipped...]
{'R': 0.010416666666666666, 'Pi': None, 'D': None, 'He': 0.3762886597938144, 'Aing': 2}
{'R': 0.01020408163265306, 'Pi': None, 'D': None, 'He': 0.37105751391465686, 'Aing': 2}
{'R': 0.010309278350515464, 'Pi': None, 'D': None, 'He': 0.3736587418472543, 'Aing': 2}
[...skipped...]

In this example, we recycled a unique Site instance using its method from_align() instead of creating a new instance at each iteration step, which is a good practice for performance reasons in this precise sitution. Note that there is also a process_sites() method to process a list of sites in one call. process_sites() is more appropriate to process dynamically generated arrays of sites as in this case.

Pi and D are not computed because they are not defined for individual sites. What we really want, in this example, is to replicate the analysis performed with process_align() to demonstrate how it would be done if we had only individual sites in the first place. This can be achieved by means of the multi argument:

>>> cs.configure(multi=False, struct=struct)
>>> for i in range(aln1.ls):
...     site.from_align(aln1,i)
...     stats = cs.process_site(site)
>>> print(cs.results())
{'He': 0.02184674638703229, 'Aing': 1.098813786929275, 'R': 0.0010210126233630454, 'Pi': 185.90085077948126, 'D': 0.47716739584524404}

Static list of sites

Linkage disequilibrium statistics, as well as \(\bar{r}_d\) (code rD), require that all sites used for analysis are available at the time of final computation. Those statistics cannot be computed by the method results() of ComputeStats if the data have been provided by process_site() or process_sites(). The examples below demonstrates it with the case of the ZnS statistic. Such statistic can be computed if we pass an Align:

>>> cs.clear_stats()
>>> cs.add_stats('ZnS')
>>> print(cs.process_align(aln1))
{'ZnS': 0.17236275214525582}

They can be as well if we pass several fragments, but only if they have the same number of samples (it is implied that the list of samples is matching, that is that data are phased):

>>> alnA = aln1.extract(0, 4500)
>>> alnB = aln1.extract(4500, None)
>>> cs.configure(multi=True)
>>> cs.set_structure(struct)
>>> cs.process_align(alnA)
>>> cs.process_align(alnB)
>>> print(cs.results())
{'ZnS': 0.17236275214525582}

To test what happens when we provide the sites individually, we extract all sites of the alignment. However, process_align() excludes by default all sites with any missing data in the ingroup while process_site() considers all sites which are provided. So we need to filter the sites ourselves, to only include those that have no missing data, hence 99 available samples, using the class Freq:

>>> sites = []
>>> frq = egglib.Freq()
>>> for i in range(aln1.ls):
...     site = egglib.site_from_align(aln1, i)
...     frq.from_site(site, struct)
...     if frq.nseff(frq.ingroup) == 99:
...         sites.append(site)

The statistics in question are not computed if we provide the sites individually and one by one, regardless of whether they are phased or not, because nothing guarantees that the site objects will be constant until statistics are actually computed:

>>> for site in sites:
...     cs.process_site(site)
>>> print(cs.results())
{'ZnS': None}

In that case, it is necessary to pass all sites grouped together in one list:

>>> print(cs.process_sites(sites))
{'ZnS': 0.17236275214525582}

Site frequency spectrum

A function is dedicated to computing the site frequency spectrum (SFS) out of a set of sites. The sites can be provided as a list of Site instances or any iterable yielding Site instances such as those provided by Align.iter_sites() or VCF.iter_sites().

Below, we use the latter tool to screen a VCF file and compute the SFS using all sites:

>>> import egglib
>>> vcf = egglib.io.VCF('LG15.bcf')
>>> sfs = egglib.stats.SFS(vcf.iter_sites())
>>> print(sfs)
[0, 252, 155, 137, 125, 106, 69, 55, 46, 58, 44, 62, 45, 92, 67,
 101, 50, 46, 92, 39, 34, 43, 23, 14, 42, 29, 23, 36, 49, 23, 18,
 26, 10, 26, 19, 45, 33, 36, 39, 13, 8, 5, 7, 4, 1, 1, 5, 3, 9, 3,
 4, 17, 21, 3, 10, 6, 9, 11, 3, 15, 28, 22, 18, 17, 18, 24, 22, 14,
 36, 13, 16, 24, 28, 28, 22, 29, 28, 14, 13, 3]

With the help of the matplotlib module, we can represent this SFS graphically:

>>> from matplotlib import pyplot
>>> pyplot.stem(sfs, linefmt='k', basefmt='k')
>>> pyplot.xlabel('Absolute frequency')
>>> pyplot.ylabel('Number of sites')

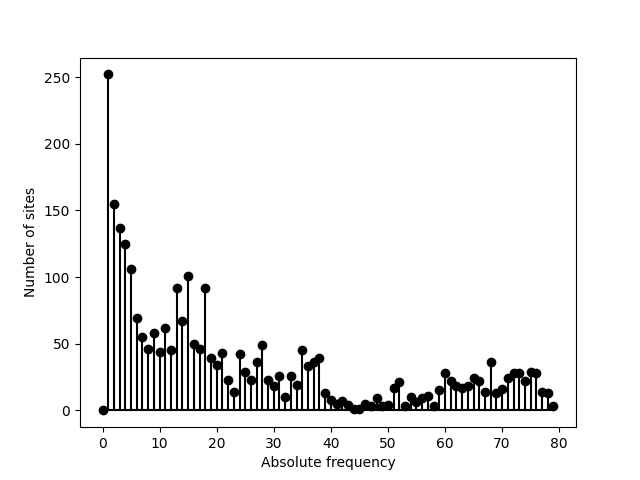
Now imagine we process a dataset with many fixed sites such as the alignment generated by this particular simulation:

>>> coalsim = egglib.coalesce.Simulator(num_pop=1, num_chrom=[100], theta=100, num_sites=10000)
>>> aln = coalsim.simul()
>>> sfs = egglib.stats.SFS(aln.iter_sites())
>>> print(sfs)
[9533, 98, 47, 32, 8, 21, 12, 13, 29, 3, 3, 3, 22, 0, 21, 41, 0, 3,
 8, 0, 1, 0, 0, 95, 1, 0, 2, 0, 0, 0, 1, 0, 0, 0, 0, 2, 0, 0, 0, 0,
 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>> pyplot.clf()
>>> pyplot.stem(sfs, linefmt='k', basefmt='k')
>>> pyplot.xlabel('Absolute frequency')
>>> pyplot.ylabel('Number of sites')
>>> pyplot.savefig('SFS-2.png')

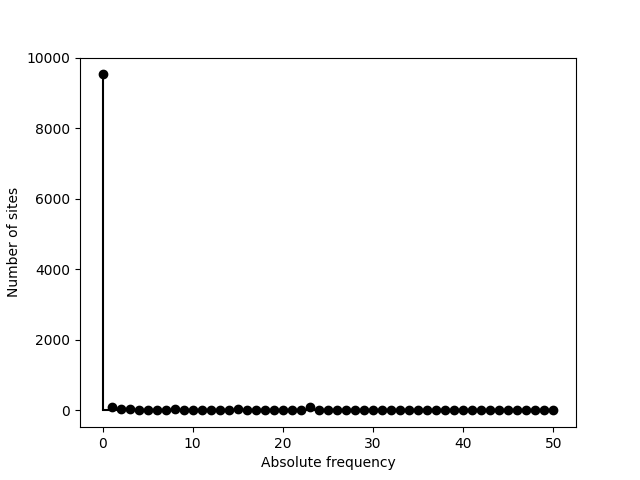
Ignoring the fixed sites can be an option. The corresponding category is set to None (instead of being removed), avoiding a shift of indexes of the returned list and allowing a direct plot of the result:

>>> sfs = egglib.stats.SFS(aln.iter_sites(), skip_fixed=True)
>>> print(sfs)
[None, 98, 47, 32, 8, 21, 12, 13, 29, 3, 3, 3, 22, 0, 21, 41, 0, 3,
 8, 0, 1, 0, 0, 95, 1, 0, 2, 0, 0, 0, 1, 0, 0, 0, 0, 2, 0, 0, 0, 0,
 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>> pyplot.clf()
>>> pyplot.stem(sfs, linefmt='k', basefmt='k')
>>> pyplot.xlabel('Absolute frequency')
>>> pyplot.ylabel('Number of sites')
>>> pyplot.savefig('SFS-3.png')

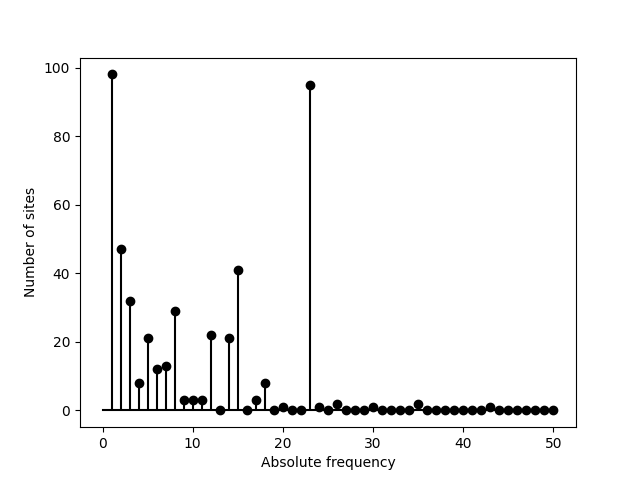
If an outgroup is available a unfolded SFS can be generated. We perform a new simulation with a separate population with a single sample that will be used as outgroup. Since we pass a Structure object containing an outgroup, the unfolded SFS is compute automatically:

>>> coalsim = egglib.coalesce.Simulator(num_pop=2, num_chrom=[40, 1], theta=100, num_sites=10000)
>>> coalsim.params.add_event(T=4, cat='merge', src=0, dst=1)
>>> struct = egglib.struct_from_samplesizes([40], outgroup=1)
>>> aln = coalsim.simul()
>>> sfs = egglib.stats.SFS(aln.iter_sites(), skip_fixed=True, struct=struct)
>>> pyplot.clf()
>>> pyplot.stem(sfs, linefmt='k', basefmt='k')
>>> pyplot.xlabel('Absolute frequency')
>>> pyplot.ylabel('Number of sites')
>>> pyplot.savefig('SFS-4.png')

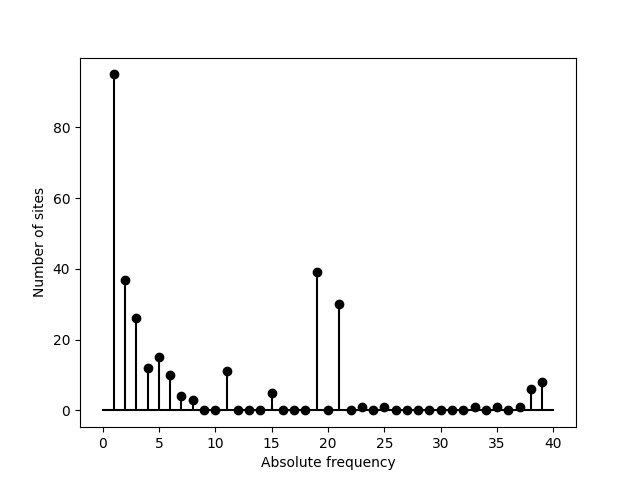
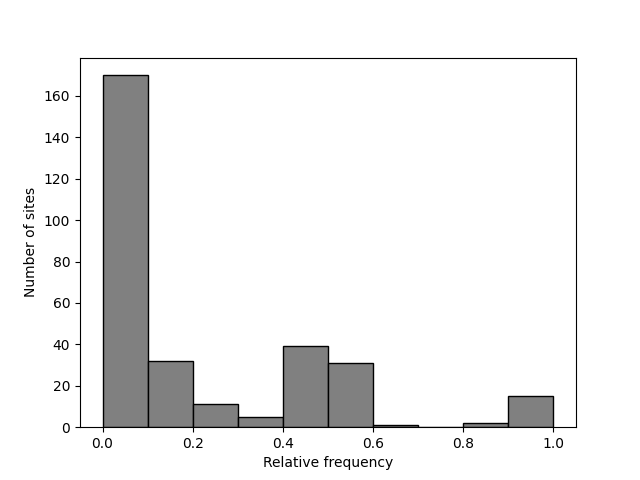
A binarized SFS can also be generated. The return value is then a list of tuples containing the upper bound and the count value. Binarized SFS might be better displayed as a bar plot so we use the bounds from the returned list to place the bars and set the width of the bars to the bin size (using a negative value for because we need to provide the position of left corner of the bars and we have the upper bounds):

>>> sfs = egglib.stats.SFS(aln.iter_sites(), skip_fixed=True, struct=struct, nbins=10)
>>> print(sfs)
[(0.1, 170), (0.2, 32), (0.3, 11), (0.4, 5), (0.5, 39), (0.6, 31),
 (0.7, 1), (0.8, 0), (0.9, 2), (1.0, 15)]
>>> pyplot.clf()
>>> x, y = zip(*sfs)
>>> pyplot.bar(x=x, height=y, width=-0.1, align='edge', color='0.5', edgecolor='k')
>>> pyplot.xlabel('Relative frequency')
>>> pyplot.ylabel('Number of sites')
>>> pyplot.savefig('SFS-5.png')

Stand-alone allelic frequencies

It can happen that only allelic frequencies are available (such as with bulk sequencing). In that case Site is not appropriate because it requires an ordering of samples. It would be possible to arbitrarily create a site from a set of allelic frequencies but this would be a pointless waste of computing resources. There is a class in EggLib, named Freq, addressing this case.

There is a logical relationship between the classes Align, Site, and Freq: the latter two can be created based on instances of the respective previous one, but they can also be provided by external means. In other words, Align and even Site can be bypassed if the corresponding data are not available. We have seen in the previous section that it is not necessary to artifically create an Align instance if only available sites are available. Likewise, Site can be bypassed if only frequencies are available.

Like Site, Freq instances can be created from different types of source: from a Site instance, from a user-specified list, or from VCF data.

Generator functions	Source of data
freq_from_site()	A Site instance.
freq_from_list()	A user-provided list of data.
freq_from_vcf()	The current data of a VCF parser (see Using VCF files).

There are also equivalent methods to recycle an existing instance.

Creation of Freq instances from a site

If we go back to the example site created above, we see that creating a Freq instance is rather straighforward (see highlighted line below):

>>> site = egglib.site_from_list(
...     ['C', 'G', 'G', 'C', 'T', 'T', 'G', 'T', 'G', 'G', 'G', 'G'],
...     alphabet=egglib.alphabets.DNA)
>>> freq = egglib.freq_from_site(site)
>>> for i in range(freq.num_alleles):
...     print(freq.allele(i), freq.freq_allele(i))
C 2
G 7
T 3

Creation of Freq instances from user-provided frequency data

To create a Freq instance from already computed allelic frequencies, the syntax is logical but the data format must be followed carefully. Here, it is necessary to provide allelic or genotypic frequencies while taking into account population structure. Formally, freq_from_list() expects allelic population frequencies for an arbitrary number of clusters (at least one). The number of alleles, of clusters, and of populations per clusters are deduced from provided data. In practice, this requires that you provide a nested list of frequencies with three levels: clusters, populations, individuals.

The basic structure of the input nested list is:

• First level: [cluster1, cluster2, ...]

• Second level: cluster1 = [pop1, pop2, ...]

• Third level: pop1 = [p1, p2, ...] where p1 is the absolute frequency of the first allele (the number of allele must match over all populations.

In many cases, there will be no clusters, which is actually equivalent to a single cluster. In this case, the first level would be a list containing a single item: [[pop1, pop2, ...]].

It is possible also that there is no population structure. Then this level can be also bypassed by using a single-item list.

The outgroup is loaded as the second argument, and is provided as another list that is analogous to an additional population (a list of frequencies of all alleles, even if there is only one sample).

Actually, for simple cases, the syntax is not verbose. The above example, assuming a single cluster and a single population, while providing allelic frequencies only, writes as follows:

>>> freq = egglib.freq_from_list([[[3, 3, 2, 1, 1]]], [1, 0, 0, 0, 0])

If your data are based on genotypes, you can provide genotypic frequencies. In this case you are required to provided as well a list detailing the allele composition of each genotypes considered. In the example above, there are also five genotypes, but each is represented by a single copy. We need to recode them, and use the geno_list option:

>>> freq = egglib.freq_from_list([[[1, 1, 1, 1, 1]]], [1, 0, 0, 0, 0],
...         geno_list=[(0, 0), (0, 1), (2, 2), (3, 1), (1, 4)],
...         alphabet=egglib.alphabets.positive_infinite)

The allelic frequencies are computed automatically based on the composition of genotypes as provided.

Computing diversity statistics

Using the same example as above, we can see that we can also compute diversity statistics for a single site or from an array of sites when only frequencies are available (obviously, statistics requiring haplotypic information will not be available). For this we need to use the method process_freq() of ComputeStats:

>>> cs.clear_stats()
>>> cs.add_stats('Aing', 'He', 'R')
>>> site = egglib.site_from_align(aln1, 66)
>>> freq = egglib.freq_from_site(site)
>>> print(cs.process_freq(freq))
{'He': 0.6178217821782178, 'Aing': 3, 'R': 0.02}
>>> cs.add_stats('D', 'Pi')
>>> cs.configure(multi=True)
>>> cs.set_structure(struct)
>>> site = egglib.Site()
>>> freq = egglib.Freq()
>>> for i in range(aln1.ls):
...     site.from_align(aln1,i)
...     freq.from_site(site)
...     cs.process_freq(freq)
>>> print(cs.results())
{'Aing': 1.1378886155222545, 'Pi': 193.00524876495805, 'He': 0.023322406154947233, 'D': -0.4440572753610234, 'R': 0.0013951963115034285}